Geometric progression

Diagram illustrating three basic geometric sequences of the pattern 1(rⁿ⁻¹) up to 6 iterations deep. The first block is a unit block and the dashed line represents the infinite sum of the sequence, a number that it will forever approach but never touch: 2, 3/2, and 4/3 respectively.

A geometric progression, also known as a geometric sequence, is a mathematical sequence of non-zero numbers where each term after the first is found by multiplying the previous one by a fixed number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression with a common ratio of 3. Similarly 10, 5, 2.5, 1.25, ... is a geometric sequence with a common ratio of 1/2.

Examples of a geometric sequence are powers r^k of a fixed non-zero number r, such as 2^k and 3^k. The general form of a geometric sequence is

$a,\ ar,\ ar^{2},\ ar^{3},\ ar^{4},\ \ldots$

where r is the common ratio and a is the initial value.

The sum of a geometric progression's terms is called a geometric series.

Properties

The nth term of a geometric sequence with initial value a = a₁ and common ratio r is given by

$a_{n}=a\,r^{n-1},$

and in general

$a_{n}=a_{m}\,r^{n-m}.$

Geometric sequences satisfy the linear recurrence relation

$a_{n}=r\,a_{n-1}$ for every integer $n>1.$

This is a first order, homogeneous linear recurrence with constant coefficients.

Geometric sequences also satisfy the nonlinear recurrence relation

$a_{n}=a_{n-1}^{2}/a_{n-2}$ for every integer $n>2.$

This is a second order nonlinear recurrence with constant coefficients.

When the common ratio of a geometric sequence is positive, the sequence's terms will all share the sign of the first term. When the common ratio of a geometric sequence is negative, the sequence's terms alternate between positive and negative; this is called an alternating sequence. For instance the sequence 1, −3, 9, −27, 81, −243, ... is an alternating geometric sequence with an initial value of 1 and a common ratio of −3. When the initial term and common ratio are complex numbers, the terms' complex arguments follow an arithmetic progression.

If the absolute value of the common ratio is smaller than 1, the terms will decrease in magnitude and approach zero via an exponential decay. If the absolute value of the common ratio is greater than 1, the terms will increase in magnitude and approach infinity via an exponential growth. If the the absolute value of the common ratio equals 1, the terms will stay the same size indefinitely, though their signs or complex arguments may change.

Geometric progressions show exponential growth or exponential decline, as opposed to arithmetic progressions showing linear growth or linear decline. This comparison was taken by T.R. Malthus as the mathematical foundation of his An Essay on the Principle of Population. The two kinds of progression are related through the exponential function and the logarithm: exponentiating each term of an arithmetic progression yields a geometric progression, while taking the logarithm of each term in a geometric progression yields an arithmetic progression.

Geometric series

Proof without words of the formula for the sum of a geometric series – if |r| < 1 and n → ∞, the rⁿ term vanishes, leaving S_∞ = ⁠a/1 − r⁠

This section is an excerpt from Geometric series.[edit]

The geometric series 1/4 + 1/16 + 1/64 + 1/256 + ... shown as areas of purple squares. Each of the purple squares has 1/4 of the area of the next larger square (1/2×1/2 = 1/4, 1/4×1/4 = 1/16, etc.). The sum of the areas of the purple squares is one third of the area of the large square.

Another geometric series (coefficient a = 4/9 and common ratio r = 1/9) shown as areas of purple squares. The total purple area is S = a / (1 - r) = (4/9) / (1 - (1/9)) = 1/2, which can be confirmed by observing that the unit square is partitioned into an infinite number of L-shaped areas each with four purple squares and four yellow squares, which is half purple.

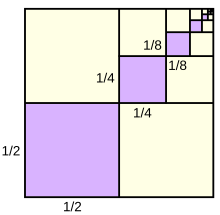
In mathematics, a geometric series is a series in which the ratio of successive adjacent terms is constant. In other words, the sum of consecutive terms of a geometric sequence forms a geometric series. Each term is therefore the geometric mean of its two neighbouring terms, similar to how the terms in an arithmetic series are the arithmetic means of their two neighbouring terms.

Geometric series have been studied in mathematics from at least the time of Euclid in his work, Elements, which explored geometric proportions. Archimedes further advanced the study through his work on infinite sums, particularly in calculating areas and volumes of geometric shapes (for instance calculating the area inside a parabola) and the early development of calculus, where they have been paradigmatic examples of both convergent series and divergent series. They serve as prototypes for frequently used mathematical tools such as Taylor series, Fourier series, and matrix exponentials.

Geometric series have been applied to model a wide variety of natural phenomena and social phenomena, such as the expansion of the universe where the common ratio between terms is defined by Hubble's constant, the decay of radioactive carbon-14 atoms where the common ratio between terms is defined by the half-life of carbon-14, probabilities of winning in games of chance where the common ratio could be determined by the odds of a roulette wheel, and the economic values of investments where the common ratio could be determined by a combination of inflation rates and interest rates.

In general, a geometric series is written as $a+ar+ar^{2}+ar^{3}+...$, where $a$ is the initial term and $r$ is the common ratio between adjacent terms. For example, the series

${\frac {1}{2}}\,+\,{\frac {1}{4}}\,+\,{\frac {1}{8}}\,+\,{\frac {1}{16}}\,+\,\cdots$

is geometric because each successive term can be obtained by multiplying the previous term by $1/2$.

Truncated geometric series $a+ar+ar^{2}+ar^{3}+\dots +ar^{n}$ are called "finite geometric series" in certain branches of mathematics, especially in 19th century calculus and in probability and statistics and their applications.

The standard generator form expression for the infinite geometric series is

$a+ar+ar^{2}+ar^{3}+\dots =\sum _{k=0}^{\infty }ar^{k}$

and the generator form expression for the finite geometric series is

$a+ar+ar^{2}+ar^{3}+\dots +ar^{n}=\sum _{k=0}^{n}ar^{k}.$

Any finite geometric series has the sum $a(1-r^{n+1})/(1-r)$, and when $|r|<1$ the infinite series converges to the value $a/(1-r)$.

Though geometric series are most commonly found and applied with the real or complex numbers for $a$ and $r$, there are also important results and applications for matrix-valued geometric series, function-valued geometric series, p-adic number geometric series, and, most generally, geometric series of elements of abstract algebraic fields, rings, and semirings.

Product

The infinite product of a geometric progression is the product of all of its terms. The partial product of a geometric progression up to the term with power $n$ is

$$\prod _{k=0}^{n}ar^{(k)}=a^{n+1}r^{n(n+1)/2}.$$

When $a$ and $r$ are positive real numbers, this is equivalent to taking the geometric mean of the partial progression's first and last individual terms and then raising that mean to the power given by the number of terms $n+1.$

$$\prod _{k=0}^{n}ar^{k}=a^{n+1}r^{n(n+1)/2}=({\sqrt {a^{2}r^{n}}})^{n+1}{\text{ for }}a\geq 0,r\geq 0.$$

This corresponds to a similar property of sums of terms of a finite arithmetic sequence: the sum of an arithmetic sequence is the number of terms times the arithmetic mean of the first and last individual terms. This correspondence follows the usual pattern that any arithmetic sequence is a sequence of logarithms of terms of a geometric sequence and any geometric sequence is a sequence of exponentiations of terms of an arithmetic sequence. Sums of logarithms correspond to products of exponentiated values.

Proof

Let $P_{n}$ represent the product up to power $n$. Written out in full,

$P_{n}=a\cdot ar\cdot ar^{2}\cdots ar^{n-1}\cdot ar^{n}$.

Carrying out the multiplications and gathering like terms,

$P_{n}=a^{n+1}r^{1+2+3+\cdots +(n-1)+n}$.

The exponent of r is the sum of an arithmetic sequence. Substituting the formula for that sum,

$P_{n}=a^{n+1}r^{\frac {n(n+1)}{2}}$,

which concludes the proof.

One can rearrange this expression to

$P_{n}=(ar^{\frac {n}{2}})^{n+1}.$

Rewriting a as $\textstyle {\sqrt {a^{2}}}$ and r as $\textstyle {\sqrt {r^{2}}}$ though this is not valid for $a<0$ or $r<0,$

$P_{n}=({\sqrt {a^{2}r^{n}}})^{n+1}{\text{ for }}a\geq 0,r\geq 0$

which is the formula in terms of the geometric mean.

History

A clay tablet from the Early Dynastic Period in Mesopotamia (c. 2900 – c. 2350 BC), identified as MS 3047, contains a geometric progression with base 3 and multiplier 1/2. It has been suggested to be Sumerian, from the city of Shuruppak. It is the only known record of a geometric progression from before the time of old Babylonian mathematics beginning in 2000 BC.

Books VIII and IX of Euclid's Elements analyze geometric progressions (such as the powers of two, see the article for details) and give several of their properties.

See also

• Arithmetic progression – Sequence of equally spaced numbers
• Arithmetico-geometric sequence – Mathematical sequence satisfying a specific pattern
• Linear difference equation
• Exponential function – Mathematical function, denoted exp(x) or e^x
• Harmonic progression – Progression formed by taking the reciprocals of an arithmetic progression
• Harmonic series – Divergent sum of all positive unit fractions
• Infinite series – Infinite sum
• Preferred number – Standard guidelines for choosing exact product dimensions within a given set of constraints
• Thomas Robert Malthus – British political economist (1766–1834)
• Geometric distribution – Probability distribution

References

• Hall & Knight, Higher Algebra, p. 39, ISBN 81-8116-000-2

External links

• "Geometric progression", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Derivation of formulas for sum of finite and infinite geometric progression at Mathalino.com
• Geometric Progression Calculator Archived 2008-12-27 at the Wayback Machine
• Nice Proof of a Geometric Progression Sum at sputsoft.com
• Weisstein, Eric W. "Geometric Series". MathWorld.